El año 2018 fue proclamado el Año Internacional de la Biología Matemática. Los objetivos de esta celebración fueron el señalar la importancia de la aplicación de las matemáticas a la biología y a las ciencias de la vida y fomentar esta interacción. De hecho, no se pueden concebir hoy en día las ciencias de la vida sin ese aporte matemático, que va desde el uso de los sistemas dinámicos y la estadística, a los modelos de población y de propagación de enfermedades. Los modelos matemáticos son representaciones simplificadas de la estructura y del funcionamiento de un determinado sistema o proceso biológico, utilizando el lenguaje matemático para expresar las relaciones entre variables.
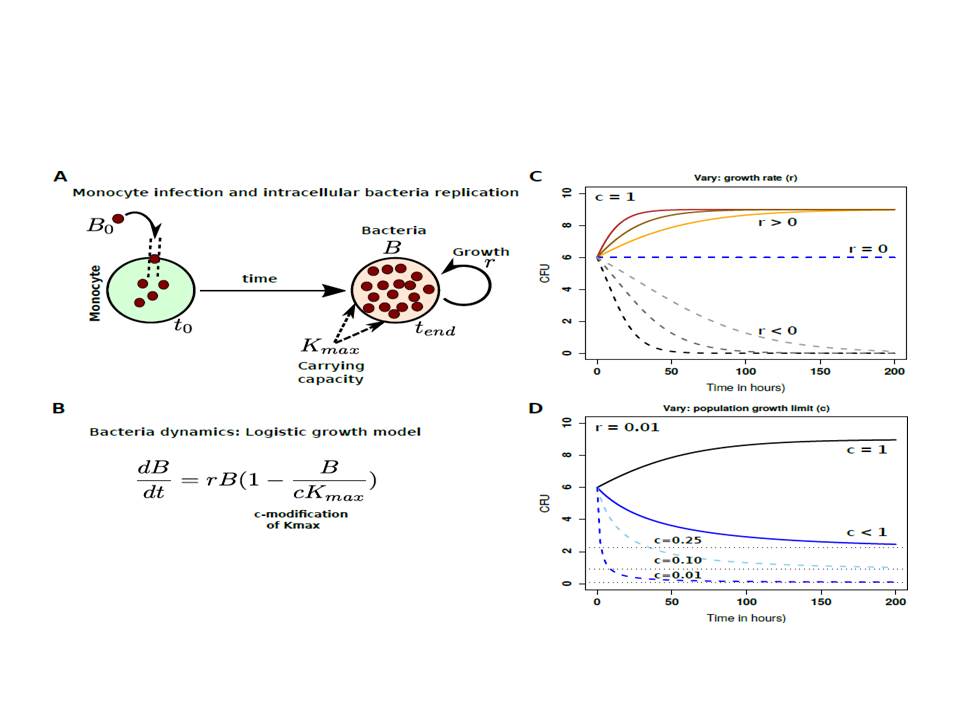
En el departamento de Sanidad Animal de NEIKER hemos publicado un estudio en el Journal of Theoretical Biology en el que se describe la generación y utilidad de tres modelos matemáticos para descifrar las variables implicadas en la virulencia de distintos aislados de Mycobacterium avium subsp paratuberculosis (Map) en macrófagos animales. Además, los modelos matemáticos generados permitieron, predecir la evolución de la carga bacteriana y su correlación con la progresión de la infección. Para este estudio se ha utilizado la base de datos generada durante la realización de la tesis doctoral de Naiara Abendaño que contiene más de 485 registros experimentales correspondientes a unidades formadoras de colonias obtenidas tras la infección de tres modelos de infección in vitro de macrófagos con 10 aislados distintos de Map. A partir de estos datos experimentales se generaron tres modelos: un modelo de crecimiento logístico no-lineal basado en ecuaciones diferenciales ordinarias (ODE), un modelo lógico no-lineal basado en redes neuronales y un modelo estadístico general lineal (GLM). Los tres modelos confirmaron que los macrófagos bovinos y ovinos presentan distinta susceptibilidad a la infección por Map; que el genotipo de cada aislado de Map no parece influir en la virulencia de éste, y que los aislados de Map presentan distinta virulencia atendiendo a su tasa de multiplicación en los macrófagos infectados. El modelo ODE predijo que los aislados de Map procedentes de bovinos y de animales silvestres (gamo, bisonte, jabalí) son capaces de crecer en macrófagos bovinos y ovinos, y de establecer infecciones progresivas caracterizadas por un aumento progresivo de la carga bacteria en los macrófagos infectados y la consiguiente necrosis celular, liberación de bacteria viable al espacio extracelular, reclutamiento de nuevos macrófagos al sitio de la infección, e inducción de una respuesta inmune inflamatoria. En contraste, los aislados de Map procedentes de pequeños rumiantes o no crecieron o crecieron mínimamente en un bajo número de macrófagos bovinos y ovinos dando lugar a un tipo de infección no-progresiva y anti-destructiva, en donde la bacteria puede persistir durante un largo periodo de tiempo en el interior de los macrófagos infectados y las respuestas inmunes pro- y anti inflamatorias aparecen balanceadas.
Para más información podéis acceder directamente a la versión final del artículo en Science Direct a través de este link. Además de para descifrar la virulencia de distintos aislados de Map, los modelos matemáticos generados en este estudio podrían ayudar a estimar la supervivencia de cepas Map en los macrófagos del hospedador tras la administración de diversos inmunomoduladores, vacunas o agentes terapéuticos, así como las dosis y tiempo de administración más adecuados. Este trabajo es un buen ejemplo de cómo los modelos matemáticos son excelentes herramientas para entender las interacciones bacteria-hospedador y los procesos biológicos.